Bab.6 Rekursi
|
Tujuan Instruksional
|
|
|
·
Menjelaskan apa itu metode rekursif dan
keuntungan menggunakannya.
·
Mengembangkan metode rekursif untuk
fungsi-fungsi matematik rekursif.
·
Menjelaskan bagaimana pemanggilan metode
rekursif ditangani di dalam tumpukan pemanggilan.
·
Menggunakan suatu metode helper teroverload
untuk menderivasi suatu metode rekursif.
|
·
Menyelesaikan pengurutan seleksi menggunakan
rekursi.
·
Menyelesaikan pencarian biner menggunakan
rekursi.
·
Mendapatkan ukuran direktori menggunakan
rekursi.
·
Menyelesaikan masalah Menara Hanoi menggunakan
rekursi.
·
Menggambar fraktal menggunakan rekursi.
·
Menyelesaikan masalah Delapan Ratu menggunakan
rekursi.
|
6.1
Introduksi
Dimisalkan Anda sedang mencari seluruh file
di bawah suatu direktori yang memuat suatu kata tertentu. Bagaimana Anda
menyelesaikan masalah ini? Ada beberapa cara untuk melakukannya. Solusi efektif
adalah menggunakan rekursi dengan mencari file-file yang diinginkan di dalam
semua subdirektori secara rekursif.
Teka-teki Delapan Ratu klasik adalah
bagaimana menempatkan delapan ratu dalam suatu papan catur sehingga tidak ada
dua ratu yang saling serang (yaitu, tidak ada dua ratu berada dalam baris sama,
kolom sama, atau diagonal sama), seperti tertampil pada Gambar 6.1. Bagaimana
Anda menulis program untuk menyelesaikan masalah ini? Pendekatan yang efektif
adalah menggunakan rekursi.
Gambar 6.1 Teka-teki Delapan Ratu dapat diselesaikan
menggunakan rekursi
Menggunakan rekursi berarti memprogram
menggunakan metode rekursif, yaitu metode, yang secara langsung ataupun tidak
langsung, memanggil dirinya sendiri. Rekursi merupakan suatu teknik pemrograman
yang sangat bermanfaat. Dalam beberapa kasus, rekursi memampukan Anda untuk
solusi efektif dan sederhana atas masalah-masalah yang kompleks. Bab ini akan
mengenalkan Anda konsep dan teknik pemrograman rekursif dan memberikan beberapa
ilustrasi untuk membantu Anda untuk berpikir secara rekursif.
6.2
Masalah: Menghitung Faktorial
Banyak
fungsi matematik yang didefinisikan menggunakan rekursi. Akan dimulai dari
suatu contoh sederhana. Faktorial suatu angkan n dapat didefinisikan secara rekursif sebagai berikut:
Bagaimana
Anda mencari n! atas suatu n? Untuk mencari 1! mudah, karena Anda mengetahui bahwa 0! sama dengan 1, dan 1! adalah 1
0!. Bila
diasumsikan bahwa Anda mengetahui (n - 1)!,
maka Anda bisa mendapatkan n!,
menggunakan n
(n - 1)!. Jadi,
masalah menghitung n! direduksi
menjadi masalah menghitung (n – 1)!.
Ketika menghitung (n – 1)!, Anda
bisa menerapkan ide yang sama secara rekursif sampai n direduksi menjadi 0.
Dimisalkan
bahwa faktorial(n) merupakan metode
untuk menghitung n!. Jika Anda
memanggil metode tersebut dengan n = 0,
maka metode tersebut dengan segera memberikan nilai balik. Metode tersebut
tentunya bisa menyelesaikan kasus yang paling sederhana, yang dikenal dengan kasus basis atau kondisi penghenti. Jika Anda memanggil metode tersebut dengan n > 0, maka masalah akan direduksi
menjadi submasalah untuk menghitung faktorial atas n – 1. Submasalah ini pada intinya sama dengan masalah pokok,
tetapi hanya lebih sederhana dan lebih kecil. Karena submasalah memiliki watak
yang sama dengan masalah asli, Anda bisa memanggil metode dengan argumen yang
berbeda, yang dikenal dengan suatu pemanggilan
rekursif.
Algoritma
rekursif untuk menghitung faktorial(n) dapat dengan sederhana dijelaskan
sebagai berikut:
if (n
== 0)
return 1;
else
return n * faktorial(n
- 1);
Suatu
pemanggilan rekursif dapat menghasilkan lebih banyak lagi pemanggilan rekursif,
karena metode dapat terus membagi suatu submasalah menjadi sub-submasalah yang
baru. Untuk menghentikan metode rekursif, masalah akhirnya harus direduksi
menjadi suatu kasus basis atau kasus penghenti, dimana pada saat itu metode
mengembalikan hasil kepada pemanggilnya. Proses rekursif berlanjut sampai hasil
dilewatkan kembali kepada pemanggil awal. Masalah awal dapat diselesaikan
dengan mengalikan n dengan faktorial(n-1).
Kode6.1 HitungFaktorial.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
import java.util.Scanner;
public class HitungFaktorial {
/** Metode utama */
public static void main(String[]
args) {
// Menciptakan suatu Scanner
Scanner masukan = new
Scanner(System.in);
System.out.print("Masukkan suatu
integer non-negatif: ");
int n = masukan.nextInt();
// Menampilkan faktorial
System.out.println("Faktorial dari
" + n + " adalah "+ faktorial(n));
}
/** Mengembalikan nilai faktorial untuk
suatu nilai tertentu */
public static long faktorial(int n){
if (n == 0) // Kasus basis
return 1;
else
return n * faktorial(n - 1); //
Pemanggilan rekursif
}
}
|
Keluaran
Masukkan suatu integer non-negatif:
5
Faktorial dari 5 adalah 120
Masukkan suatu integer
non-negatif: 10
Faktorial dari 10 adalah
3628800
Metode faktorial (baris 16-21) secara esensi
merupakan penterjemahan atas definisi matematik atas faktorial menjadi kode
JAVA. Pemanggilan terhadap faktorial
bersifat rekursif karena memanggil dirinya sendiri. Parameter yang dilewatkan
kepada metode faktorial didekremen
sampai dicapainya kasus basis.
Gambar
6.2 mengilustrasikan eksekusi atas beberapa pemanggilan rekursif, dimulai dari n = 4. Kegunaan memori tumpukan
ditampilkan pada Gambar 6.3.
Jika
rekursi tidak mereduksi masalah dengan suatu cara sehingga tidak terjadi
konvergensi menjadi kasus basis, maka rekursi tak-berhingga akan terjadi.
Sebagai contoh, dimisalkan Anda menuliskan secara salah metode faktorial sebagai berikut:
public static long faktorial(int n) {
return n * faktorial(n - 1);
}
Pada
kasus ini, metode faktorial akan berjalan secara tak-berhingga dan menyebabkan
suatu StackOverflowError.
Gambar
6.2 Pemanggilan faktorial(4) menyebabkan beberapa pemanggilan rekursif terhadap
metode faktorial
Gambar
6.3 Ketika faktorial(4) sedang dieksekusi, metode faktorial dipanggil secara
rekursif, menyebabkan memori tumpukan berubah secara dinamis
6.3
Masalah: Menghitung Bilangan Fibonacci
Metode faktorial pada bagian terdahulu dapat
dengan mudah ditulis-ulang tanpa menggunakan rekursi. Dalam beberapa kasus,
penggunaan rekursi memampukan Anda untuk menyajikan solusi yang efektif dan
sederhana atas permasalahan yang sulit untuk diselesaikan. Perhatikan deret
Fibonacci berikut ini:
deret: 0 1 1 2 3 5 8 13 21 34 55 89 ...
indeks: 0 1 2 3
4 5
6 7 8 9 10 11
Deret
Fibonacci dimulai dengan 0 dan 1, dengan setiap subruntun angka merupakan
penjumlahan dari dua angka sebelumnya. Runtun ini dapat secara rekursif
didefinisikan sebagai berikut:
fib(0) = 0;
fib(1) = 1;
fib(indeks) = fib(indeks - 2)
+ fib(indeks - 1); indeks >= 2
Deret
Fibonacci dinamai oleh Leonardo Fibonacci, seorang matematikawan abad
pertengahan, yang mulai memodelkannya untuk menghitung pertumbuhan populasi
kelinci. Deret ini dapat pula digunakan untuk optimisasi numerik dan berbagai
aplikasi lain.
Bagaimana
Anda mencari fib(indeks) atau suatu indeks yang diberikan? Adalah hal mudah
untuk menghitung fib(2), karena Anda
mengetahui fib(1) dan fib(0). Diasumsikan bahwa Anda telah
mengetahui fib(indeks-2) dan fib(indeks-1), maka Anda bisa
menghitung fib(indeks) dengan mudah.
Oleh karena itu, masalah menghitung fib(indeks)
direduksi menjadi masalah menghitung fib(indeks-2)
dan fib(indeks-2). Ketika
melakukannya, Anda menerapkan ide rekursif sampai indeks direduksi menjadi 1 dan 0.
Kasus
basis adalah indeks = 0 atau indeks = 1. Jika Anda memanggil metode fib dengan indeks = 0 atau indeks = 1,
maka akan menghasilkan nilai balik dengan segera. Jika Anda memanggil metode
tersebut dengan indeks >= 2, maka
masalah akan dibagi menjadi dua submasalah untuk menghitung fib(indeks-1) dan fib(indeks-2) menggunakan pemanggilan rekursif. Algoritma rekursif
untuk menghitung fib(indeks) dapat
dengan sederhana dideskripsikan sebagai berikut:
if (indeks
== 0)
return 0;
else if (indeks
== 1)
return 1;
else
return fib(indeks
- 1) + fib(indeks - 2);
Kode6.20
menyajikan suatu program utuh yang meminta pengguna untuk memasukkan suatu
indeks dan yang menghitung bilangan Fibonacci atas indeks tersebut.
Kode6.2 HitungFibonacci.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
import java.util.Scanner;
public class HitungFibonacci {
/** Metode utama */
public static void main(String
args[]) {
// Menciptakan suatu Scanner
Scanner masukan = new Scanner(System.in);
System.out.print("Masukkan suatu
indeks untuk bilangan Fibonacci: ");
int indeks = masukan.nextInt();
// Mencari dan menampilkan bilangan
Fibonacci
System.out.println(
"Bilangan Fibonacci pada indeks
" + indeks + " adalah " + fib(indeks));
}
/** Metode untuk mencari bilangan Fibonacci
*/
public static long fib(long indeks){
if (indeks == 0) // Kasus basis
return 0;
else if (indeks == 1) // Kasus
basis
return 1;
else // Reduksi dan pemanggilan
rekursif
return fib(indeks - 1) + fib(indeks - 2);
}
}
|
Keluaran
Masukkan suatu indeks untuk
bilangan Fibonacci: 10
Bilangan Fibonacci pada
indeks 10 adalah 55
Masukkan suatu indeks untuk
bilangan Fibonacci: 20
Bilangan Fibonacci pada
indeks 20 adalah 6765
Program
tidak menampilkan beban kerja di belakang layar oleh komputer. Gambar 6.4
menyajikan pemanggilan rekursif berurutan dalam mengevaluasi fib(4). Metode awal, fib(4), melakukan dua pemanggilan
rekursif, fib(3) dan fib(2), dan menghasilkan nilai balik fib(3) + fib(2). Tetapi dengan urutan
bagaimana metode-metode ini dipanggil? Pada JAVA, operand-operand dievaluasi
dari kiri ke kanan. fib(2) dipanggil
setelah fib(3) selesai dievaluasi.
Label-label pada Gambar 6.4 menunjukkan urutan metode-metode tersebut
dipanggil.
Seperti
tertampil pada Gambar 6.4, terdapat banyak pemanggilan rekursif terduplikasi.
Sebagai contoh, fib(2) dipanggil dua
kali, fib(1) tiga kali, dan fib(0) dua kali. Pada umumnya,
penghitungan fib(indeks) memerlukan
kira-kira dua kali pemanggilan rekursif daripada penghitungan fib(indeks-1). Jika Anda mencoba indeks
yang jauh lebih besar, maka jumlah pemanggilan bertambah secara signifikan. Di
samping jumlah pemanggilan yang bertambah, komputer juga memerlukan waktu dan
memori untuk menjalankan metode-metode rekursif.
Gambar
6.4 Pemanggilan fib(4) menyebabkan beberapa pemanggilan rekursif terhadap metode fib
6.4
Menyelesaikan Masalah Menggunakan Rekursi
Bagian-bagian
terdahulu menyajikan dua rekursi klasik. Semua metode rekursi memiliki beberapa
karakteristik sebagai berikut:
·
Metode diimplementasikan menggunakan stateman if-else
atau switch yang mengarah pada
kasus-kasus yang berbeda.
·
Satu atau lebih kasus basis (kasus paling sederhana) digunakan
untuk menghentikan rekursi.
·
Setiap rekursi mereduksi masalah awal, membawanya
secara menaik lebih dekat ke suatu kelas basis sampai menjadi kasus tersebut.
Pada
umumnya, untuk menyelesaikan suatu masalah menggunakan rekursi, Anda memecahnya
menjadi beberapa submasalah. Setiap submasalah hampir sama dengan masalah awal
tetapi lebih kecil dalam ukuran. Anda bisa menerapkan pendekatan yang sama
terhadap setiap submasalah untuk menyelesaikannya secara rekursif.
Sekarang
pertimbangkan masalah sederhana dalam menampilkan suatu pesan sebanyak n kali. Anda memecah masalah ini
menjadi dua submasalah: Satu untuk menampilkan pesan sebanyak sekali dan
submasalah lainnya adalah untuk menampilkan sebanyak n - 1 kali. Masalah kedua sama dengan masalah awal namun dengan
ukuran yang lebih kecil. Kasus basis untuk masalah ini adalah n==0. Anda dapat menyelesaikan masalah
ini menggunakan rekursi sebagai berikut:
public static void nPrintln(String
pesan, int kali)
{
if (kali >= 1)
{
System.out.println(pesan);
nPrintln(pesan, kali - 1);
} // Kasus basis adalah kali == 0
}
Perhatikan
bahwa metode fib pada contoh
terdahulu mengembalikan suatu nilai kepada pemanggilnya, tetapi metode nPrintln bertipe void, jadi tidak mengembalikan nilai balik.
Jika
Anda berpikir secara rekursif, Anda dapat menggunakan rekursi untuk
menyelesaikan banyak masalah yang disajikan. Perhatikan kasus palindrome. Ingat
bahwa string dikatakan suatu palindrome bila menghasilkan suatu string yang
sama jika dibaca dari kiri maupun dari kanan. Sebagai contoh, ada dan apa merupakan palindrome, tetapi ayah dan ibu bukan
palindrome. Masalah memeriksa apakah suatu string palindrome atau tidak dapat
dibagi menjadi dua submasalah:
·
Memeriksa apakah karakter pertama dan karakter terakhir
string adalah sama atau tidak.
·
Mengabaikan dua karakter akhir dan memeriksa apakah
sisa substring adalah suatu palindrome atau tidak.
Submasalah
kedua sama dengan masalah awal dengan ukuran yang lebih kecil. Terdapat dua kasus
basis: (1) dua karakter akhir tidak sama; (2) ukuran string adalah 0 atau 1.
Pada kasus (1), string bukan palindrome; dan pada kasus (2), string adalah
palindrome. Metode rekursif untuk masalah ini dapat diimplementasikan pada
kode6.3.
Kode6.3 PlindromeRekursifMenggunakanSubstring.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public class PalindromeRekursifMenggunakanSubstring {
public static boolean apaPalindrome(String s) {
if (s.length() <= 1) // Kasus
basis
return true;
else if (s.charAt(0) !=
s.charAt(s.length() - 1)) // Kasus basis
return false;
else
return apaPalindrome(s.substring(1, s.length() - 1));
}
public static void main(String[]
args) {
System.out.println("Apakah mama
suatu palindrome? "
+ apaPalindrome("mama"));
System.out.println("Apakah papa suatu
palindrome? "
+ apaPalindrome("papa"));
System.out.println("Apakah a suatu
palindrome? " + apaPalindrome("a"));
System.out.println("Apakah aba
suatu palindrome? "
+
apaPalindrome("aba"));
System.out.println("Apakah ab
suatu palindrome? " + apaPalindrome("ab"));
}
}
|
Keluaran
Apakah
mama suatu palindrome? false
Apakah
papa suatu palindrome? false
Apakah a
suatu palindrome? true
Apakah
aba suatu palindrome? true
Apakah
ab suatu palindrome? false
Metode substring pada baris 8 menciptakan
suatu string baru yang sama dengan string awal kecuali bahwa tidak terdapat
karakter awal dan akhir. Pemeriksaan apakah suatu string palindrome atau tidak
ekivalen dengan apakah substring palindrome atau tidak jika kedua karakter
ujung pada string awal adalah sama.
6.5
Metode Helper Rekursif
Metode apaPalindrome rekursif terdahulu tidak
efisien, karena menciptakan suatu string baru untuk setiap pemanggilan
rekursif. Untuk menghindarinya, Anda dapat menggunakan indeks tinggi dan rendah
untuk mengindikasikan rentang substring. Kedua indeks tersebut kemudian dilewatkan
kepada metode rekursif. Karena metode awal adalah apaPalindrome(String s), Anda perlu menciptakan suatu metode baru apaPalindrome(String s, int rendah, int
tinggi) untuk menerima informasi tambahan pada string, seperti ditunjukkan
pada kode6.4.
Kode6.4 PalindromeRekursif.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
public class PalindromeRekursif {
public static boolean apaPalindrome(String s) {
return apaPalindrome(s, 0,
s.length() - 1);
}
public static boolean apaPalindrome(String s, int rendah, int
tinggi) {
if (tinggi <= rendah)// Kasus basis
return true;
else if (s.charAt(rendah) != s.charAt(tinggi)) //
Kasus basis
return false;
else
return apaPalindrome(s, rendah +
1, tinggi - 1);
}
public static void main(String[]
args) {
System.out.println("Apakah mama
adalah suatu palindrome? "
+ apaPalindrome("mama"));
System.out.println("Apakah papa
suatu palindrome? "
+ apaPalindrome("papa"));
System.out.println("Apakah a suatu
palindrome? " + apaPalindrome("a"));
System.out.println("Apakah
aba suatu palindrome? " +
apaPalindrome("aba"));
System.out.println("Apakah ab
suatu palindrome? " + apaPalindrome("ab"));
}
}
|
Keluaran
Apakah
mama suatu palindrome? false
Apakah
papa suatu palindrome? false
Apakah a
suatu palindrome? true
Apakah
aba suatu palindrome? true
Apakah
ab suatu palindrome? false
Dua
metode apaPalindrome teroeverload
didefinisikan. Yang pertama, apaPalindrome(String
s), memeriksa apakah suatu string palindrome atau tidak, dan yang kedua, apaPalindrome(String s, int rendah, int
tinggi), memeriksa apakah suatu substring s(rendah..tinggi) palindrome atau tidak. Metode pertama melewatkan
string s dengan rendah = 0 dan tinggi =
s.length() - 1 kepada metode kedua. Metode kedua dapat dipanggil secara
rekursif.
Metode
helper sangat berguna dalam solusi rekursif untuk masalah-masalah yang
melibatkan string dan array. Beberapa bagian ke depan akan menyajikan dua
contoh lagi.
6.5.1
Pengurutan Seleksi
Pengurutan
seleksi digunakan untuk mencari angka terkecil di dalam suatu daftar dan
kemudian menempatkannya di awal daftar tersebut. Kemudian pengurutan ini
mencari angka terkecil yang tersisa dan menempatkannya setelah angka terkecil
pertama, dan seterusnya sampai daftar hanya memuat satu angka yang tersisa.
Masalah ini dapat dibagi menjadi dua submasalah:
·
Mencari angka terkecil di dalam daftar dan menukarnya
dengan angka pertama.
·
Mengabaikan angka pertama dan mengurutkan daftar sisa
yang lebih kecil secara rekursif.
Kelas
basis adalah ketika daftar hanya memuat satu angka yang tersisa. Kode6.5
menyajikan contoh metode pengurutan seleksi.
Kode6.5 PengurutanSeleksiRekursif.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
public class PengurutanSeleksiRekursif {
public static void urut(double[]
daftar) {
urut(daftar, 0, daftar.length - 1);// Mengurutkan seluruh isi
daftar
}
public static void urut(double[] daftar, int rendah, int tinggi) {
if (rendah < tinggi) {
// Mencari angka terkecil dan indeksnya di dalam
daftar(rendah .. tinggi)
int indeksDariMin = rendah;
double min = daftar[rendah];
for (int i = rendah + 1; i
<= tinggi; i++) {
if (daftar[i] < min) {
min = daftar[i];
indeksDariMin = i;
}
}
// Menukar angka
terkecil di dalam daftar(rendah .. tinggi) dengan daftar(rendah)
daftar[indeksDariMin] = daftar[rendah];
daftar[rendah] = min;
// Mengurutkan sisa daftar(rendah+1 ..
tinggi)
urut(daftar, rendah + 1, tinggi);
}
}
}
|
Dua
metode urut teroverload
didefinisikan. Metode pertama, urut(double[]
daftar), mengurutkan suatu array di dalam daftar[0..daftar.length()-1] dan metode kedua, urut(double[] daftar, int rendah, int tinggi) mengurutkan suatu
array di dalam daftar[rendah..tinggi].
Metode kedua dapat dipanggil secara rekursif untuk mengurutkan suatu subarray
menyusut.
6.5.2
Pencarian Biner
Untuk
melakukan pencarian biner, elemen-elemen di dalam array harus diurutkan.
Pencarian biner pertama-tama membandingkan kunci di dalam elemen di tengah
array. Perhatikan tiga kasus berikut:
·
Kasus 1: Jika kunci lebih rendah dari elemen tengah,
kunci di dalam setengah array pertama dicari secara rekursif.
·
Kasus 2: Jika kunci sama dengan elemen tengah,
pencarian biner berakhir dengan suatu kecocokan.
·
Kasus 3: Jika kunci lebih besar dari elemen tengah, kunci
di dalam setengah array kedua dicari secara rekursif.
Kasus 1
dan kasus 3 mereduksi pencarian menjadi suatu daftar pencarian yang lebih
kecil. Kasus 2 merupakan kasus basis ketika ditemukan suatu kecocokan. Kasus
basis lainnya adalah bahwa pencarian berakhir tanpa kecocokan. Kode6.6
menyajikan suatu contoh solusi sederhana dan jelas atas masalah pencarian biner
menggunakan rekursi.
Kode6.6 PencarianBinerRekursif.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
public class PencarianBinerRekursif {
public static int PencarianBinerRekursif(int[] daftar, int kunci) {
int rendah = 0;
int tinggi = daftar.length - 1;
return
PencarianBinerRekursif(daftar, kunci, rendah, tinggi);
}
public static int PencarianBinerRekursif(int[] daftar, int kunci,
int rendah, int tinggi) {
if (rendah > tinggi)// Daftar
telah dicari tanpa ada kecocokan
return -rendah - 1;
int tengah = (rendah + tinggi) / 2;
if (kunci < daftar[tengah])
return PencarianBinerRekursif(daftar, kunci, rendah, tengah - 1);
else if (kunci == daftar[tengah])
return tengah;
else
return
PencarianBinerRekursif(daftar, kunci, tengah + 1, tinggi);
}
}
|
Metode
pertama mencari suatu kunci di dalam keseluruhan daftar. Metode kedua mencari
suatu kunci di dalam daftar dengan indeks rendah
sampai tinggi.
Metode PencarianBinerRekursif pertama
melewatkan array awal dengan rendah = 0
dan tinggi = daftar.length() – 1
kepada metode PencarianBinerRekursif
kedua. Metode kedua dapat dipanggil secara rekursif untuk mencari kunci di
dalam subarray menyusut.
6.6
Masalah: Mencari Kapasitas Suatu Direktori
Beberapa
contoh terdahulu dapat dengan mudah diselesaikan tanpa menggunakan rekursi. Bagian
ini akan menyajikan suatu masalah yang sulit diselesaikan tanpa menggunakan
rekursi. Tantangan di sini adalah mencari kapasitas atau ukuran suatu
direktori. Kapasitas suatu direktori adalah penjumlahan ukuran semua file di
dalam direktori. Suatu direktori d
bisa saja memuat beberapa subdirektori. Dimisalkan suatu direktori memuat
beberapa file f1, f2, ..., fm dan beberapa direktori d1, d2, ..., dn, seperti
tertampil pada Gambar 6.5.
Gambar
6.5 Suatu direktori memuat beberapa
file dan beberapa direktori
Kapasitas
direktori dapat didefinisikan secara rekursif sebagai berikut:
kap(d) =
kap(f1) + kap(f2) +...+ kap(fm) + kap(d1) + kap(d2) +...+ kap(dn)
Kelas File dapat digunakan untuk
merepresentasikan suatu file atau suatu direktori dan dapat memperoleh properti
file dan direktori. Dua metode di dalam kelas File berguna untuk masalah ini:
·
Metode length()
mengembalikan kapasitas suatu file.
·
Metode listFile()
mengembalikan suatu array yang memuat objek-objek File di bawah suatu direktori.
Kode6.7
menyajikan suatu program yang meminta pengguna untuk memasukkan suatu direktori
atau suatu file dan menampilkan kapasitasnya.
Kode6.7 KapasitasDirektori.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
import java.io.File;
import java.util.Scanner;
public class KapasitasDirektori {
public static void main(String[]
args) {
// Meminta pengguna untuk memasukkan suatu
file atau direktori
System.out.print("Masukkan suatu
direktori atau file: ");
Scanner masukan = new
Scanner(System.in);
String direktori = masukan.nextLine();
// Menampilkan kapasitas
System.out.println(getSize(new File(direktori)) + " byte");
}
public static long getSize(File file) {
long kapasitas = 0; // Menyimpan
kapasitas total semua file
if(file.isDirectory()) {
File[] files = file.listFiles();// Semua
file dan subdirektori
for (int i = 0; i <
files.length; i++) {
kapasitas += getSize(files[i]); //
Pemanggilan rekursif
}
}
else { // Kasus basis
kapasitas += file.length();
}
return kapasitas;
}
}
|
Keluaran
Masukkan suatu direktori
atau file: E:\BUKU SELESAI DITULIS
6323035721 byte
Masukkan suatu direktori
atau file: E:\yamaguchi.bmp
589878 byte
Masukkan suatu direktori
atau file: E:\filetidakada
0 byte
Jika
objek file merepresentasikan suatu
direktori (baris 18), maka setiap subitem (file atau direktori) di dalam
direktori tersebut dipanggil secara rekursif untuk mendapatkan kapasitasnya
(baris 21). Jika objek file
merepresentasikan suatu file (baris 24), maka kapasitas file diperoleh (baris
25).
Apa yang
terjadi bila direktori salah atau direktori yang tidak ada dientrikan? Program
akan mendeteksi dengan memanggil file.length()
(baris 25), yang mengembalikan 0. Jadi, pada kasus ini, metode getSize() akan mengembalikan 0.
6.7
Masalah: Menara Hanoi
Masalah
menara Hanoi merupakan suatu masalah klasik yang dapat diselesaikan dengan
mudah menggunakan rekursi tetapi cukup sulit diselesaikan bila tanpa rekursi.
Gambar
6.6 Tantangan menara Hanoi adalah
memindahkan semua disk dari menara A ke menara B tanpa mengabaikan
aturan-aturan yang ditetapkan
Masalah
ini melibatkan aksi untuk memindahkan sejumlah disk tertentu dengan berbagai
ukuran dari satu menara ke menara lain dengan mentaati beberapa aturan sebagai
berikut:
·
Terdapat n
buah disk berlabel 1, 2, 3,...,n dan
tiga menara berlabel A, B, dan C.
·
Tidak ada disk yang berada di atas suatu disk lebih
kecil pada sembarang waktu.
·
Semua disk awalnya ditempatkan pada menara A.
·
Hanya satu disk yang boleh digerakkan atau dipindahkan
pada suatu waktu, dan disk tersebut harus berada di atas suatu menara.
Tujuan
tantangan ini adalah untuk memindahkan semua disk dari menara A ke menara B
dengan bantuan menara C. Sebagai contoh, jika Anda memiliki tiga disk, maka
beberapa langkah yang dibutuhkan untuk memindahkan semua disk dari menara A ke
menara B ditampilkan pada Gambar 6.6.
Pada
kasus tiga disk, Anda dapat menemukan solusi secara manual. Untuk jumlah disk
yang lebih besar, bahkan bila hanya empat disk, masalah menjadi cukup kompleks.
Beruntung bahwa masalah ini bisa diselesaikan secara rekursif.
Gambar
6.7 Masalah
menara Hanoi dapat didekomposisi menjadi tiga submasalah
Kasus
basis untuk masalah ini adalah n = 1.
Jika n == 1, maka Anda hanya perlu
memindahkan disk dari A ke B. Jika n
> 1, maka Anda perlu memecah masalah awal menjadi tiga submasalah dan
menyelesaikannya secara sekuensial.
1. Memindahkan
n – 1 disk pertama dari A ke C
dengan bantuan menara B, seperti tertampil pada Gambar 6.7.
2. Memindahkan
n disk dari A ke B, seperti
tertampil pada langkah 2 pada Gambar 6.7.
3. Memindahkan
n – 1 disk dari C ke B dengan bantuan menara A, seperti tertampil pada langkah
3 pada Gambar 6.7.
Metode
berikut memindahkan n disk dari dariMenara ke keMenara dengan bantuan bantuanMenara:
void pindahDisk(int
n, char dariMenara,
char keMenara, char
bantuanMenara)
Algoritma
untuk metode ini dapat dideskripsikan sebagai berikut:
if (n
== 1) // Kondisi penghenti
Memindahkan disk 1 dari dariMenara ke keMenara;
else {
pindahDisk(n - 1,
dariMenara, bantuanMenara, keMenara);
Memindahkan n disk dari dariMenara ke keMenara;
pindahDisk (n - 1,
bantuanMenara, keMenara, dariMenara);
}
Kode6.8
menyajikan suatu contoh yang meminta pengguna untuk memasukkan sejumlah disk
dan yang memanggil metode rekursif pindahDisk
untuk menampilkan solusi dalam memindahkan disk-disk yang diberikan.
Kode6.8 MenaraHanoi.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
import java.util.Scanner;
public class MenaraHanoi {
/** Metode utama */
public static void main(String[]
args) {
// Menciptakan suatu Scanner
Scanner masukan = new
Scanner(System.in);
System.out.print("Masukkan
sejumlah disk: ");
int n = masukan.nextInt();
// Mencari solusi secara rekursif
System.out.println("Perpindahan
yang dilakukan adalah:");
pindahDisk(n, 'A', 'B', 'C');
}
/** Metode untuk mencari solusi untuk
memindahkan n disk
dari dariMenara ke keMenara dengan bantuan
bantuanMenara */
public static void pindahDisk(int n, char
dariMenara,
char keMenara, char bantuanMenara) {
if (n == 1) // Kondisi penghenti
System.out.println("Memindahkan disk"
+ n + " dari " +
dariMenara + " ke " +
keMenara);
else {
pindahDisk(n - 1, dariMenara, bantuanMenara, keMenara);
System.out.println("Memindahkan disk
" + n + " dari " +
dariMenara + " ke " +
keMenara);
pindahDisk(n - 1, bantuanMenara, keMenara, dariMenara);
}
}
}
|
Keluaran
Masukkan sejumlah disk: 4
Perpindahan yang dilakukan
adalah:
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 3 dari A
ke C
Memindahkan disk 1 dari B
ke A
Memindahkan disk 2 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 4 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 2 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 3 dari C
ke B
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Masukkan sejumlah disk: 6
Perpindahan yang dilakukan
adalah:
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 3 dari A
ke C
Memindahkan disk 1 dari B
ke A
Memindahkan disk 2 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 4 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 2 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 3 dari C
ke B
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 5 dari A
ke C
Memindahkan disk 1 dari B
ke A
Memindahkan disk 2 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 3 dari B
ke A
Memindahkan disk 1 dari C
ke B
Memindahkan disk 2 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 4 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 3 dari A
ke C
Memindahkan disk 1 dari B
ke A
Memindahkan disk 2 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 6 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 2 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 3 dari C
ke B
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 4 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 2 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 3 dari B
ke A
Memindahkan disk 1 dari C
ke B
Memindahkan disk 2 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 5 dari C
ke B
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 3 dari A
ke C
Memindahkan disk 1 dari B
ke A
Memindahkan disk 2 dari B
ke C
Memindahkan disk 1 dari A
ke C
Memindahkan disk 4 dari A
ke B
Memindahkan disk 1 dari C
ke B
Memindahkan disk 2 dari C
ke A
Memindahkan disk 1 dari B
ke A
Memindahkan disk 3 dari C
ke B
Memindahkan disk 1 dari A
ke C
Memindahkan disk 2 dari A
ke B
Memindahkan disk 1 dari C
ke B
Masalah
ini secara inheren rekursif. Penggunaan rekursi menjadikan solusi sederhana.
Akan menjadi susah untuk diselesaikan bila tanpa menggunakan rekursi.
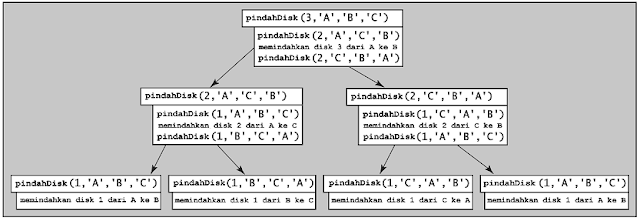
Gambar
6.8 Pemanggilan pindahDisk(3, ‘A, ‘B’, ‘C’)
menyebabkan pemanggilan pindahDisk
secara rekursif
Perhatikan
penjejakan program untuk n = 3.
Pemanggilan rekursif secara berurutan ditampilkan pada Gambar 6.8. Seperti yang
Anda lihat, menulis program lebih mudah daripada menjejak pemanggilan rekursif.
Sistem menggunakan tumpukan untuk menjejak beberapa pemanggilan di balik layar.
Pada beberapa kasus, rekursi memberikan suatu level abstraksi yang
menyembunyikan iterasi dan beberapa detil lain dari pengguna.
6.8
Masalah: Fraktal
Fraktal
merupakan suatu bangun geometrik, tetapi tidak seperti segitiga, lingkaran,
atau persegipanjang, fraktal dapat dibagi menjadi bagian-bagian, dimana setiap
bagian merupakan salinan ukuran-tereduksi dari bangun asli. Ada banyak contoh
fraktal yang menarik. Bagian ini akan mengenalkan suatu fraktal sederhana,
segitiga Sierpinski, yang dinamai oleh seorang matematikawan berkebangsaan
Polandia.
Gambar
6.9 Segitiga Sierpinski merupakan
suatu pola segitiga rekursif
Segitiga
Sierpinski diciptakan sebagai berikut:
1. Mulai
dengan suatu segitiga sama-sisi, yang dianggap sebagai fraktal Sierpinski orde
(level) 0, seperti tertampil pada Gambar 6.9a.
2. Menghubungkan
titik-titik tengah setiap sisi segitiga orde 0 untuk menciptakan segitiga
Sierpinski orde 1, seperti tertampil pada Gambar 6.9b.
3. Menghubungkan
titik-titik tengah setiap sisi dari tiga segitiga orde 1 untuk menciptakan
segitiga Sierpinski orde 2, seperti tertampil pada Gambar 6.9c.
4. Mengulangi
proses yang sama secara rekursif untuk menciptakan segitiga Sierpinski orde 3,
4, dan seterusnya (Gambar 6.9d).
Masalah
ini secara inheren rekursif. Bagaimana Anda mengembangkan solusi rekursif untuk
masalah ini? Perhatikan bahwa kelas basis adalah ketika orde 0. Sangat mudah
untuk menggambarkan suatu segitiga Sierpinski orde 0. Bagaimana Anda
menggambarkan suatu segitiga Sierpinski orde 1? Masalah ini dapat direduksi
menjadi masalah menggambarkan tiga segitiga Sierpinski orde 0. Bagaimana Anda menggambarkan
suatu segitiga Sierpinski orde 2? Masalah ini dapat direduksi menjadi masalah
menggambarkan tiga segitiga Sierpinski orde 1. Jadi masalah menggambarkan
segitiga Sierpinski orde n dapat
direduksi menjadi masalah menggambarkan tiga buah segitiga Sierpinski orde n – 1.
Kode6.9
menyajikan suatu applet JAVA yang menampilkan segitiga Sierpinski pada
sembarang orde, seperti tertampil pada Gambar 6.9. Anda bisa mengentrikan suatu
orde di dalam bidang teks untuk menampilkan segitiga Sierpinski pada suatu orde
tertentu.
Kode6.9 SegitigaSierpinski.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
import javax.swing.*;
import java.awt.*;
import java.awt.event.*;
public class SegitigaSierpinski extends JApplet {
private JTextField jtfOrde = new
JTextField("0", 5); // Orde
private PanelSegitigaSierpinski
panelSegitiga =
new PanelSegitigaSierpinski(); //
Menampilkan pola
public SegitigaSierpinski() {
// Panel untuk memuat label, bidang teks,
dan suatu tombol
JPanel panel = new JPanel();
panel.add(new JLabel("Masukkan
orde fraktal: "));
panel.add(jtfOrde);
jtfOrde.setHorizontalAlignment(SwingConstants.RIGHT);
// Menambahkan suatu panel segitiga
Sierpinski kepada applet
add(panelSegitiga);
add(panel, BorderLayout.SOUTH);
// Meregistrasi suatu listener
jtfOrde.addActionListener(new ActionListener()
{
public void actionPerformed(ActionEvent e) {
panelSegitiga.tetapkanOrde(Integer.parseInt(jtfOrde.getText()));
}
});
}
static class PanelSegitigaSierpinski extends
JPanel {
private int orde = 0;
/** Menetapkan suatu orde baru */
public void tetapkanOrde(int
orde) {
this.orde = orde;
repaint();
}
protected void
paintComponent(Graphics g) {
super.paintComponent(g);
// Memilih tiga titik proporsional
dengan ukuran panel
Point p1 = new Point(getWidth() / 2, 10);
Point p2 = new Point(10, getHeight() - 10);
Point p3 = new Point(getWidth() - 10, getHeight() - 10);
tampilSegitiga(g, orde, p1, p2, p3);
}
private static void tampilSegitiga(Graphics g, int orde,
Point p1, Point p2, Point p3) {
if (orde >= 0) {
// Menggambar suatu segitiga untuk
menghubungkan tiga titik
g.drawLine(p1.x, p1.y, p2.x, p2.y);
g.drawLine(p1.x, p1.y, p3.x, p3.y);
g.drawLine(p2.x, p2.y, p3.x, p3.y);
// Mendapatkan titik-tengah pada
setiap sisi segitiga
Point p12 = titikTengah(p1, p2);
Point p23 = titikTengah(p2, p3);
Point
p31 = titikTengah(p3, p1);
// Menampilkan secara rekursif tiga
segitiga
tampilSegitiga(g, orde - 1, p1, p12, p31);
tampilSegitiga(g, orde - 1, p12, p2, p23);
tampilSegitiga(g, orde - 1, p31, p23, p3);
}
}
private static Point
titikTengah(Point p1, Point p2) {
return new Point((p1.x + p2.x) /
2, (p1.y + p2.y) / 2);
}
}
}
|
Segitiga
awal memiliki tiga titik yang proporsional dengan ukuran panel (baris 42-44).
Metode tampilSegitiga(g, orde, p1, p2,
p3) (baris 49-67) melakukan beberapa pekerjaan sebagai berikut:
1. Menampilkan
suatu segitiga untuk menghubungkan tiga titik p1, p2, dan p3 pada baris 53-55, seperti tertampil
pada Gambar 6.10a.
2. Mendapatkan
titik tengah antara p1 dan p2 (baris 58), titik tengah antara p2 dan p3 (baris 59), dan titik tengah antara p3 dan p1 (baris 60),
seperti tertampil pada Gambar 6.10b.
3. Secara
rekursif memanggil metode tampilSegitiga
dengan suatu orde tereduksi untuk menampilkan segitiga-segitiga Sierpinski yang
lebih kecil (baris 63-66). Perhatikan bahwa setiap segitiga Sierpinski kecil
secara struktural sama dengan segitiga Sierpinski besar, seperti tertampil pada
Gambar 6.10b.
Suatu
segitiga Sierpinski ditampilkan di dalam PanelSegitigaSierpinski.
Properti orde di dalam kelas inner PanelSegitigaSierpinski menentukan orde
segitiga Sierpinski. Kelas Point
merepresentasikan suatu titik di dalam komponen. Metode titikTengah(Point p1, Point p2) mengembalikan titik tengah antara p1 dan p2 (baris 72-74).
Gambar
6.10 Penggambaran segitiga Sierpinski
menyebabkan pemanggilan untuk menggambar tiga segitiga Sierpinski secara
rekursif
6.9
Masalah: Delapan Ratu
Bagian
ini akan memberikan suatu solusi rekursif atas masalah Delapan Ratu yang
disajikan pada awal bab ini. Tantangannya adalah untuk menemukan solusi untuk
menempatkan suatu ratu pada tiap baris papan catur sehingga tidak terdapat dua
ratu yang dapat menyerang satu sama lain. Anda bisa menggunakan suatu array
dua-dimensi untuk merepresentasikan papan catur. Namun, karena setiap baris
hanya boleh memiliki satu ratu, maka hanya akan digunakan array satu-dimensi
untuk menandai posisi ratu di dalam baris. Jadi, Anda bisa mendefinisikan array
ratu sebagai berikut:
int[]
ratu = new int[8];.
Penugasan
j kepada ratu[i] dilakukan untuk menandai suatu ratu yang ditempatkan pada
baris i kolom j. Gambar 6.11a menunjukkan isi array ratu untuk papan catur pada Gambar 6.11b.
Gambar
6.11 Array ratu[i] menandai posisi ratu pada baris i
Kode6.10 DelapanRatu.java
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
import java.awt.*;
import javax.swing.*;
public class DelapanRatu extends JApplet {
public static final int UKURAN = 8;
// Ukuran papan catur
private int[] ratu = new int[UKURAN];
// Posisi ratu
public DelapanRatu() {
cari(0); // Mencari solusi dari baris 0
add(new PapanCatur(),
BorderLayout.CENTER); // Menampilkan solusi
}
/** Memeriksa apakah suatu ratu
dapat ditempatkan pada baris i dan kolom j */
private boolean apaValid(int baris, int kolom) {
for (int i = 1; i <=
baris; i++)
if (ratu[baris - i] == kolom //
Memeriksa kolom
|| ratu[baris - i] == kolom - i //
Memeriksa diagonal atas-kiri
|| ratu[baris - i] == kolom + i) //
Memeriksa diagonal atas-kanan
return false; // Ada
konflik
return true; // Tidak ada
konflik
}
/** Mencari solusi mulai dari baris tertentu
*/
private boolean cari(int baris) {
if (baris == UKURAN) //kondisi
penghenti
return
true; // Silusi ditemukan untuk menempatkan 8 ratu pada 8 baris
for (int kolom = 0; kolom
< UKURAN; kolom++) {
ratu[baris] = kolom; // Menempatkan ratu
pada (baris, kolom)
if (apaValid(baris, kolom)
&& cari(baris + 1))
return true; // Ditemukan,
mengembalikan true untuk keluar loop
}
// Tidak ada solusi untuk ratu yang ditempatkan pada
sembarang kolom pada baris ini
return false;
}
class PapanCatur extends
JPanel {
private Image citraRatu =
new ImageIcon("Gambar/ratu.gif").getImage();
PapanCatur() {
this.setBorder(BorderFactory.createLineBorder(Color.BLACK,
2));
}
protected void
paintComponent(Graphics g) {
super.paintComponent(g);
// Menggambar ratu
for (int i = 0; i <
UKURAN; i++) {
int j = ratu[i]; // Posisi ratu
pada baris i
g.drawImage(citraRatu, j * getWidth()
/ UKURAN,
i * getHeight() / UKURAN, getWidth()
/ UKURAN,
getHeight() / UKURAN, this);
}
// Menggambar garis horisontal dan
fertikal
for (int i = 1; i <
UKURAN; i++) {
g.drawLine(0, i * getHeight() /
UKURAN,
getWidth(), i * getHeight() / UKURAN);
g.drawLine(i * getWidth() / UKURAN, 0,
i * getWidth() / UKURAN,
getHeight());
}
}
}
}
|
Program
memanggil cari(0) (baris 9) untuk
memulai pencarian untuk solusi pada baris 0, yang secara rekursif memanggil cari(1), cari(2),..., dan cari(7)
(baris 30).
Metode cari(baris) mengembalikan true jika semua baris terisi (baris
25-26). Metode ini memeriksa apakah suatu ratu telah ditempatkan pada kolom 0,
1, 2, ..., dan 7 di dalam loop for
(baris 28). Kemudian program menempatkan ratu pada kolom (baris 29). Jika
penempatan valid, maka pencarian rekursif untuk baris berikutnya dilakukan
dengan memanggil cari(baris+1)
(baris 30). Jika pencarian berhasil, maka akan metode akan mengembalikan true (baris 31) agar keluar dari loop for. Pada kasus ini, tidak ada
kebutuhan untuk kolom berikutnya pada baris tersebut. Jika tidak ada solusi
agar suatu ratu ditempatkan pada sembarang kolom di dalam baris ini, maka
metode akan mengembalikan false
(baris 35).
Dimisalkan
bahwa Anda memanggil cari(baris)
untuk baris 3, seperti tertampil pada Gambar 6.12a. Metode mencoba untuk
mengisi suatu ratu pada kolom 1, 2, dan seterusnya. Untuk setiap percobaan,
metode apaValid(baris, kolom) (baris
30) dipanggil untuk memeriksa apakah penempatan suatu ratu pada posisi tertentu
akan mengakibatkan konflik atau tidak dengan ratu-ratu yang telah ditempatkan
sebelumnya. Hal ini untuk memastikan
bahwa tidak ada ratu yang ditempatkan pada kolom yang sama (baris 16),
tidak ada ratu yang ditempatkan pada diagonal atas-kiri (baris 17), tidak ada
ratu yang ditempatkan pada diagonal atas-kanan (baris 18), seperti tertampil
pada Gambar 6.12a. Jika metode apaValid(baris,
kolom) mengembalikan false, maka
kolom berikutnya akan diperiksa, seperti tertampil pada Gambar 6.12b. Jika
metode apaValid(baris, kolom)
mengembalikan true, maka metode cari(baris+1) dipanggil, seperti
tertampil pada Gambar 6.12d. Jika metode cari(baris+1) mengembalikan false,
maka kolom berikutnya pada baris terdahulu diperiksa, seperti tertampil pada
Gambar 6.12c.
Gambar
6.12 Pemanggilan cari(baris) mengisi ratu pada suatu kolom dalam baris tertentu











No comments:
Post a Comment